Fraktaler
I 1979 sad den franske matematiker Benoit Mandelbrot i kælderen i Science Centeret på Harvard Universitet med en ny Vax supermini computer. Som en ubetalt programmør havde lærerassistenten Peter Moldave tilbudt sin assistance til Mandelbrots projekt, der gik ud på at studere den tilsyneladende simple funktion: f(x) = x2 + c, hvor x og c er komplekse tal. Hertil skulle bruges computere. Det tørre computerarbejde gik i gang, og tallene manifesterede sig som billeder på computerskærmen. Pludseligt viste der sig en geometrisk figur på skærmen.
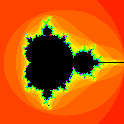
Dette billede havde forskerne forventet – teorien havde forudsagt det. Mere forundrende var en række af mindre “klatter” væk fra hovedbilledet. Ved nærmere undersøgelser så det ud som om der var tale om mindre versioner af den bille-lignende figur. Det var som om billedet reproducerede sig selv på lavere niveau! Ved at foretage mere præcise beregninger på computeren opnåedes bedre billeder, der viste flere detaljer, indtil billederne efterhånden begyndte at se mere og mere komplicerede ud.
Mandelbrot var i tvivl om, om de mystiske figurer på skærmen skyldtes det forældede grafiske udstyr i kælderen, eller der her lå en helt ny og enestående matematik gemt. For at udelukke det første afprøvede Mandelbrot programmet på en IBM mainframe computer i hans hjembase i Yorktown Heights i New York. Her i det berømmede IBM Thomas J. Watson Research Center havde Mandelbrot adgang til en imponerende computerkapacitet. På de mere avancerede computere kunne man igen se de komplicerede billeder på skærmen, blot var billederne i en bedre kvalitet.
Samtidigt afsløredes et underliggende mønster. Mandelbrot og Moldave fandt ved at zoome ind, at nogle af de små klatter på skærmen, som ved et første syn kun lignede støvpartikler, ikke var identiske versioner af den oprindelige “bille”, som de først havde troet. De var i stedet smukke og indviklede mønstre af spiraler og former, der lignede søheste.
For at forstå ovenstående må vi gribe tilbage i tiden. I 1967 havde Mandelbrot i en epokegørende artikel i magasinet Science stillet spørgsmålet: “How long is the Coastline of Britain?”. Spørgsmålet kan synes banalt i første omgang: Man kan vel bare finde et kort og måle det op! Mandelbrots pointe var imidlertid, at hvis man tager et kort med mindre målestoksforhold, altså zoomer ind på kystlinjen, så vil det, der på det forrige kort så ud til at være et forholdsvist lige stykker kystlinje, vise sig at at være krogede og bugtede kurver, med en væsentligt større længde end på det forrige kort. Sådan kunne man fortsætte med at zoome ind og få en stadig større kystlinjelængde som følge. Man kan selvfølgelig fremdrage, at denne zoomen ind må stoppe på et tidspunkt, nå man når ned til det atomare niveau eller lignende, men fra et matematisk synspunkt kan forfiningen fortsættes uendeligt. Eftersom følgen af kystlinjelængder vokser uden begrænsning med graden af zoom, følger det, at der ikke er nogen præcis matematisk definition af længden af en kystlinje.
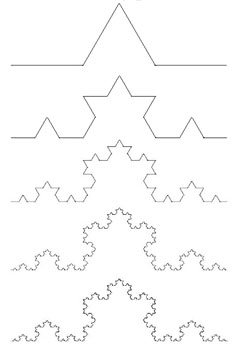
En analog situation til den britiske kystlinje, men dog en matematisk idealiseret én, fås med den såkaldte Koch-kurve, først betragtet af H. von Koch i begyndelsen af 1900-tallet. Kurven fremkommer ved følgende proces: Man starter med et linjestykke, fjerner den midterste tredjedel, og erstatter det med to linjestykker, så der dannes en spids på 60 grader, som vist på den første tegning på figuren nedenfor. Derefter gentager man arbejdet på hver af de fire linjestykker i den nye figur, dvs. erstatter den midterste tredjedel med en spids. Derved fås den anden tegning på figuren nedenfor. Processen gentages igen og igen og figurerne konvergerer efterhånden mod en “grænsefigur”, hvis udseende er meget tæt på udseendet af den femte figur nedenfor.
Også denne kurve har uendelig længde. Ordet fraktal bliver relevant idet man tildeler figurer som ovennævnte en dimension, som bliver et ikke helt tal og således bliver en udvidelse af vort sædvanlige dimensionsbegreb. I vor hverdag taler vi ofte om 1, 2 eller tre dimensioner og hvis det går rigtigt hedt til, kan vi fantasere om fire dimensioner, fx i Einsteins relativitetsteori. Men hvad er en ikke-heltallig dimension?- ja det er fraktaler!
Ordet fraktal har med brudflade og fraktur at gøre. Mens geometrien overalt har rette linier eller helt glatte kurver, synes naturen at undgå dette. Vi ser den ujævne bark, den takkede bjergkam, den uregelmæssige kyst linie. Der forekommer faktisk slet ikke helt jævne eller rette linier i naturen. Den eneste undtagelse er en lysstråle. En kystlinie er altid ujævn. Den repræsenterer både “selvsimilaritet” og “skalainvarians”, for på lang afstand ser man det samme ujævne billede som tæt på.Faktisk kan man slet ikke rigtigt definere længden af en kyststrækning, for den afhænger af, hvor lang den anvendte målestok er. Hvis vi har en målestok – altså i bogstaveligste forstand en stok man måler med – på 1 kilometer, når vi til et bestemt resultat, men vi når til et meget højere tal , dersom vi måler med en målestok på kun 1 meter. Selv om kysten er den samme, kan vi nemlig komme ind i alle små vige og krinkelkroge.

Dette, at man ikke kan få “det endelige svar”, men kan blive ved med at gå ned i stadig finere detaljer, er karakteristisk i det hele taget for fraktalgeometrien. Matematikeren Benoit Mandelbrot udfærdigede i 1979 nogle afbildninger med computer af en mængde punkter, der – viser det sig – udgør ét sammenhængende område, den berømte Mandelbrot-mængde.
Det fascinerende billede fremkommer på den måde, at man undersøger hvert punkt i xy-planet, svarende til et talpar, f. eks. x = -0.12 og y = 0.74. Dette talpar “testes” for, hvad der vil ske, når det bliver sendt gennem en formel – og det nye talpar, der kommer ud af formlen, sendes ind i formlen igen, og det nye talpar sendes ind i formlen igen…
(x,y) –> FORMEL –> (xny, yny)
Dette er netop selve iterationsprocessen. Hvis det viser sig, at talparret på et tidspunkt går mod uendeligt, vil det ikke tilhøre mængden. Hvis det – uanset hvor mange gange vi sender det igennem – forbliver inden for nogle grænser, tilhører det mængden. Talparret -0.12 0.74 ligger faktisk inden for grænserne. Computer-grafikken er altså skabt ved iteration. Den formel, der skaber netop dette billede er meget enkel. Detaljerigdommen er derfor overraskende.

Grænsedragningen på billedet er ligeså vanskelig som ved en kystlinie: Vi kan blive ved med at forstørre (ændre målestok) og se flere detaljer i randområderne. Det spændende ved disse detaljer er, at de udviser similaritet med helheden. Igen og igen kan man finde små Mandelbrot-figurer. Mandelbrotmængden udviser altså selvsimilaritet. Den udviser også skalainvarians, idet vi ser den samme figur i forskellige skalaer eller målestokke.
Vi finder også hele tiden nye former, herunder let fortegnede Mandelbrot figurer, altså en omtrentlig lighed. Afbildningerne viser en overvældende detaljerigdom. Alle disse detaljer vil først kunne studeres, når computeren har gjort sit arbejde. Der er ikke genveje til at få dem at se. De er altså, hvor utroligt det end lyder, uforudsigelige, selv om enhver detalje kan beregnes.
En anden type fraktale billeder skabes ud fra et andet princip, nemlig rekursion. Rekursionen kan typisk bestå i at gennemføre en “foldningsprocedure” igen og igen, f. eks. af et liniestykke, der så hurtigt vil udvikle sig til en “dragekurve”. Rekursion kan også bestå i at tilføje ekstra linier til en figur i en finere og finere inddeling. Dette er tilfældet i “Det tredelte træ” . Her har vi først tre rette linier, der støder sammen. Disse udgør et grundmotiv, der udmøntes igen og igen. Først udvides der med 6 nye lidt kortere linier, så vi får grundmotivet endnu 3 gange i mindre målestok. Der er i alt 9 rette linier nu. I de næste inddelinger kommer vi op på 27, 81, 243, 729 rette linier.
Og før vi nu begynder at blive alt for matematiske vil vi ende dette her afsnit om hvad fraktalker er for en størrelse med at citere Einstein; “Når alt kommer til alt er der ikke stor forskel på videnskab, kunst og religion. Efterhånden som jeg nærmere mig den sidste alder ved jeg at der er meget vi mennesker måske aldrig kommer til at forstå og de reele svar skal man måske mere søge i det spirtuelle end i det videnskabelige”.
Det som Einstein mente hermed var måske at i deres yderste konsekvenser er der ikke megen forskel mellem filosofi, matematik, kunst, musik, videnskab etc. Enhver der har kigget nærmere på eksempelvis en matematikker, der går inderligt op i sit arbejde med at udrede en formel, vil jo tydeligt kunne se at det menneske har frigjort sig fra sin traditionelle regelrette, linære tankegang og befinder sig i et holistisk tankeunivers. Et legebarn om man så må sige.

Fraktalteoriens fadder; Benoit Mandelbrot